Variational Autoencoders with Inverse Autoregressive Flows
In this post, I'm going to be describing a really cool idea about how to improve variational autoencoders using inverse autoregressive flows. The main idea is that we can generate more powerful posterior distributions compared to a more basic isotropic Gaussian by applying a series of invertible transformations. This, in theory, will allow your variational autoencoder to fit better by concentrating the stochastic samples around a closer approximation to the true posterior. The math works out so nicely while the results are kind of marginal 1. As usual, I'll go through some intuition, some math, and have an implementation with few experiments I ran. Enjoy!
Motivation
Recall in vanilla variational autoencoders (previous post), we have the generative network ("the decoder"), the posterior network ("the encoder"), which are related to each other through a set of diagonal Gaussian variables usually labelled \(z\).
In most cases, our primary objective is to train the decoder i.e. the generative model. The structure of the decoder is shown in Figure 1. We have our latent diagonal Gaussian variables, followed by a deterministic high-capacity model (i.e. deep net), which then outputs the parameters for our output variables (e.g. Bernoulli's if we're modelling black and which pixels).
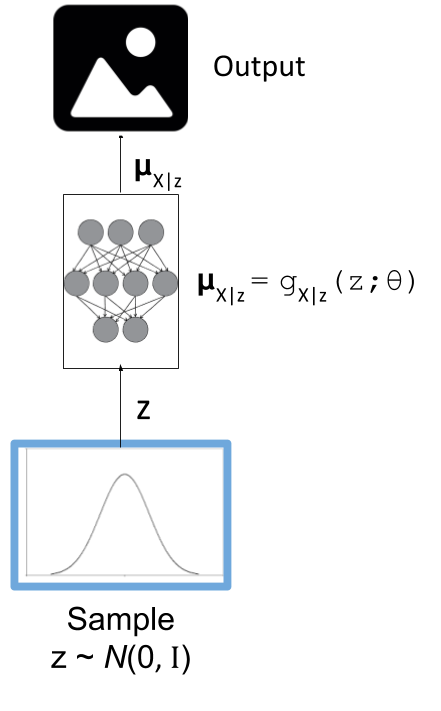
Figure 1: The generative model component of a variational autoencoder
The main problem here is that training this generative model is pretty difficult. The brute force way is to make an input/output dataset by taking each output you have (e.g. images) and cross it with a ton of random samples from \(z\). If \(z\) has many dimensions, then to properly cover the space you'll need an exponential number of examples. For example, if your number of dimensions is \(D=1\), you might need to sample roughly \((10)^1=10\) points per image, making your dataset 10x. If \(D=10\), you'll probably need \((10)^{10}\) points per image, making your dataset too big to practically train. Not only that, most of the sampled points will not contribute much to training your network because they'll be in parts of the latent space that are very low probability (with respect to the current image), contributing almost nothing to your network weights.
Of course that's exactly why variational autoencoders are so brilliant. Instead of randomly sampling from your \(z\) space, we'll use "directed" sampling to a pick point \(z\) using our encoder (or posterior) network such that \(x\) is much more likely to occur. This allows you to efficiently train your generator network. The cool thing is that we are actually training both networks simultaneously! To actually accomplish this though, we have to use fully factorized diagonal Gaussian variables and a "reparameterization trick" in order to properly get the thing to actually work (see my previous post for details). The structure is shown in Figure 2.
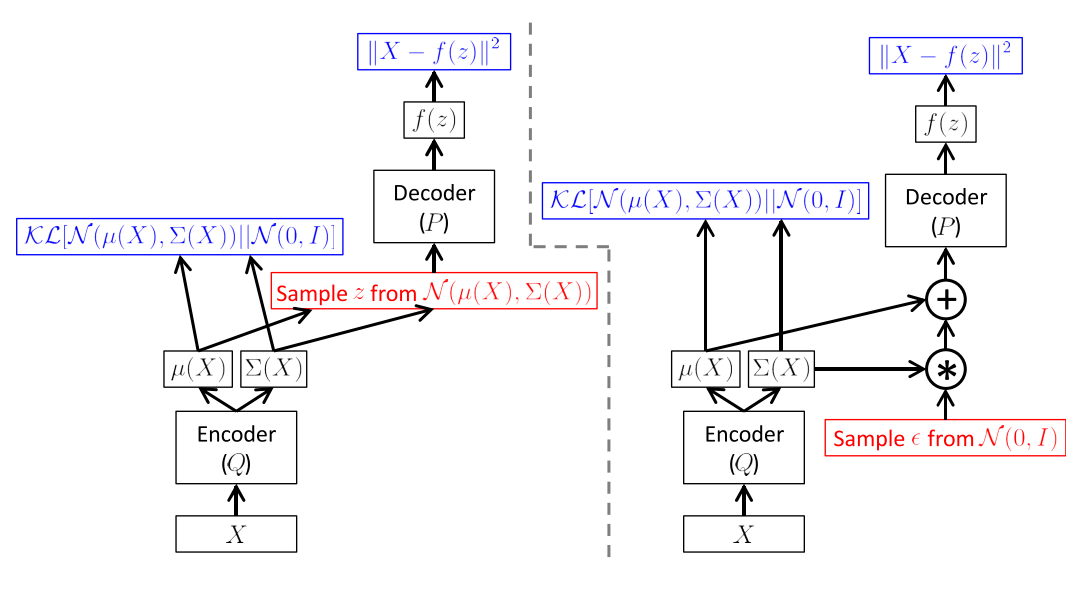
Figure 2: Left: A naive implementation of an autoencoder without the reparameterization trick. Right: A vanilla variational autoencoder with the "reparameterization trick" (Source: [4])
As you can imagine, the posterior network is an estimate of the true posterior (as is the case for variational inference methods). Unfortunately our fully factorized diagonal Gaussians can't model every distribution. In particular, the fact that they're fully factorized can limit the ability to match the true posterior we're trying to model. Theoretically if we are able to more closely approximate the true posterior, our generator network should be able to train more easily, and thus improve our overall result.
The question is how can we use a more complex distribution? The reason we're stuck with factorized Gaussians is because it is (a) computationally efficient to compute and differentiate the posterior (just backprop through the \(z\) mean and variance), and (b) it's easy to sample at every minibatch (which is just sampling from independent Gaussians because of the reparameterization trick). If we want to replace it we're going to need to still maintain these two desirable properties.
Normalizing Flows for Variational Inference
Normalizing flows in the context of variational inference was introduced by Rezende et al. in [1]. At its core, it's just applying an invertible transformation (i.e. a change of variables) to our fully factorized posterior distribution to make it into something more flexible that can match the true posterior. It's called a normalizing flow because the density "flows" through each transform. See the box below about transforming probability density functions.
Transforming Probability Density Functions
Given a n-dimensional random variable \(\bf x\) with joint density function \(f({\bf x})\), we can transform it into another n-dimensional random variable \(\bf y\) via an invertible (i.e. 1-to-1) and differentiable function \(H\) with joint density \(g({\bf y})\):
It turns out the joint density \(g({\bf y})\) can be computed as:
where the latter part of each line contains a determinant of a Jacobian. In the last line we're making it explicit that the density is a function \(\bf y\). Alternatively, we can also write this in terms of \({\bf x}\) and \(H\):
It's a bit confusing because of all the variable changing but keep in mind that you can change between \({\bf x}\) with \({\bf y}\) without much trouble because there is a 1-1 mapping. So starting from the original statement, we first apply the inverse function theorem, which allows us to re-write the Jacobian matrix in terms of \(H\) and \({\bf x}\). Next, we apply a property of determinants which says the determinant of an inverse of a matrix is just the reciprocal of the determinant of the original matrix.
It's a bit strange why we would want to put things back in terms of \({\bf x}\) and \(H\) but sometimes (like in this post) we want to evaluate \(g({\bf y})\) but don't want to explicitly compute \(H^{-1}\). Instead, it's easier to just work with \(H\).
Let's see some math to make this idea a bit more precise. Start off with a simple posterior for our initial variable, call it \(\bf z_0\). In vanilla VAEs we use a fully factorized Gaussian e.g. \(q({\bf z_0}|{\bf x}) \sim \mathcal{N}({\bf \mu(x)}, {\bf \sigma(x)})\). Next, we'll want to apply a series of invertible transforms \(f_t(\cdot)\):
Remember our posterior distribution (i.e. our encoder) is conditioned on \({\bf x}\), so we can freely use it as part of our transformation here. Using Equation 3, we can compute the (log) density of the final variable \({\bf z_t}\) as such:
Equation 5 is simply just a repeated application of Equation 3, noticing that since we're in log space the reciprocal of the determinant turns into a negative sign.
So why does this help at all? The normalizing flow can be thought of as a sequence of expansions or contractions on the initial density, allowing for things such as multi-modal distributions (something we can't do with a basic Gaussian). Additionally, it allows us to have complex relationships between the variables instead of the independence we assume with our diagonal Gaussians. The trick then is to pick a transformation \(f_t\) that gives us the flexibility, but more importantly is easy to compute because we want to use this in a VAE setup. The next section describes an elegant and simple to compute transform that accomplishes both of these things.
Inverse Autoregressive Transformations
An autoregressive transform is one where given a sequence of variables \({\bf y} = \{y_i \}_{i=0}^D\), each variable is dependent only on the previously indexed variables i.e. \(y_i = f_i(y_{0:i-1})\).
Autoregressive autoencoders introduced in [2] (and my post on it) take advantage of this property by constructing an extension of a vanilla (non-variational) autoencoder that can estimate distributions (whereas the regular one doesn't have a direct probabilistic interpretation). The paper introduced the idea in terms of binary Bernoulli variables, but we can also formulate it in terms of Gaussians too.
Recall that Bernoulli variables only have a single parameter \(p\) to estimate, but for a Gaussian we'll need two functions to estimate the mean and variance denoted by \([{\bf \mu}({\bf y}), {\bf \sigma}({\bf y})]\). However, due to the autoregressive property, the individual elements are only functions of the prior indices and thus their derivatives are zero with respect to latter indices:
Given \([{\bf \mu}({\bf y}), {\bf \sigma}({\bf y})]\), we can sequentially apply an autoregressive transform on a noise vector \(\epsilon \sim \mathcal{N}(0, {\bf I})\) as such:
where addition is element-wise and \(\odot\) is element-wise multiplication. Intuitively, this is a natural way to make Gaussians, you multiply by some standard deviation and add some mean.
However in our case, we can transform any vector, not just a noise vector. This is shown on the left hand side of Figure 3 where we take a \(\bf x\) vector and transform it to a \(\bf y\) vector. You'll notice that we have to perform \(\mathcal{O}(D)\) sequential computations, thus making it too slow for our intended purpose of use in a normalizing flow. But what about the inverse transform?
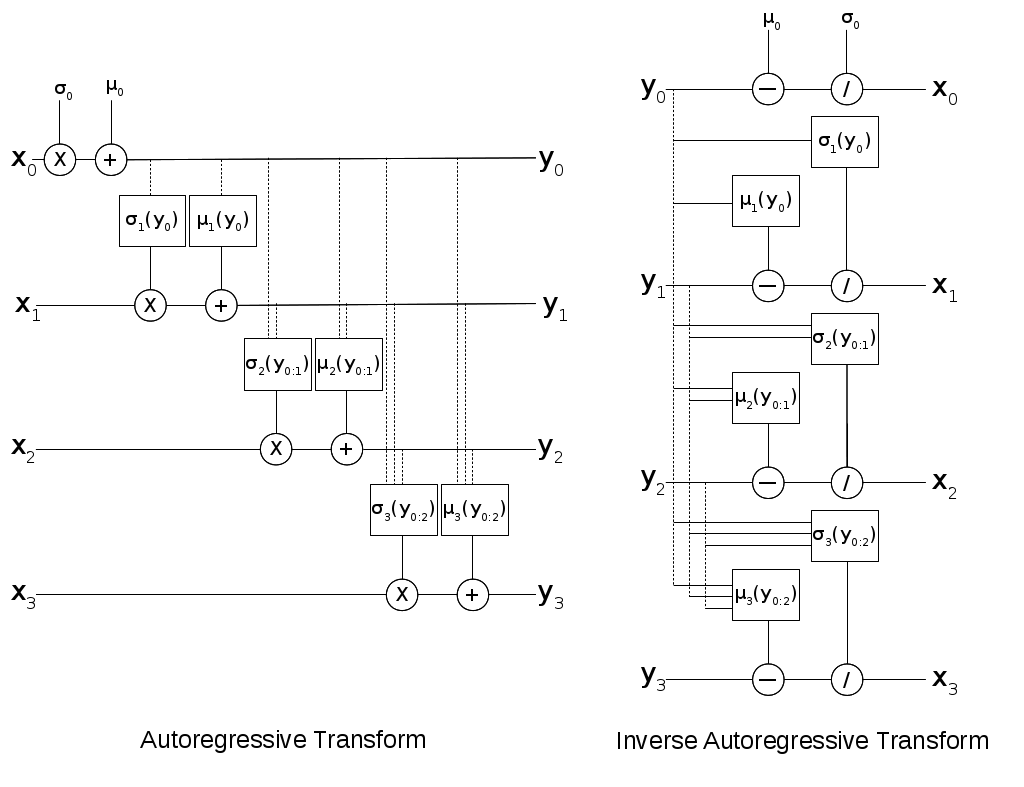
Figure 3: Gaussian version of Autoregressive Transform and Inverse Autoregressive Transforms
The inverse transform can actually be parallelized (we'll switch to \(\bf x\) as the input variable instead of \(\epsilon\)) as shown in Equation 8 and the right hand side of Figure 3 so long as we have \(\sigma_i > 0\).
where subtraction and division is element-wise.
Now here comes the beauty of this transform. Recall in normalizing flows to properly compute the probability, we have to be able to compute the determinant (or log-determinant). However, Equation 6 shows that \(\bf \mu, \sigma\) have no dependence on the current or latter variables in our sequence. Thus from Equation 8, the Jacobian is lower triangular with a simple diagonal:
Knowing that the determinant of a triangular matrix is the product of its diagonals, this gives us our final result for the log determinant which is incredibly simple to compute:
In the next section, we'll see how to use this inverse autoregressive transform to build a more flexible posterior distribution for our variational autoencoder.
Inverse Autoregressive Flows
Adding an inverse autoregressive flow (IAF) to a variational autoencoder is as simple as (a) adding a bunch of IAF transforms after the latent variables \(z\) (b) modifying the likelihood to account for the IAF transforms.
Figure 4 from [3] shows a depiction of adding several IAF transforms to a variational encoder. Two things to note: (1) a context \(h\) is additionally generated, and (2) the IAF step only involves multiplication and addition, not division and subtraction like in Equation 8. I'll explain these two points as we work through the math below.
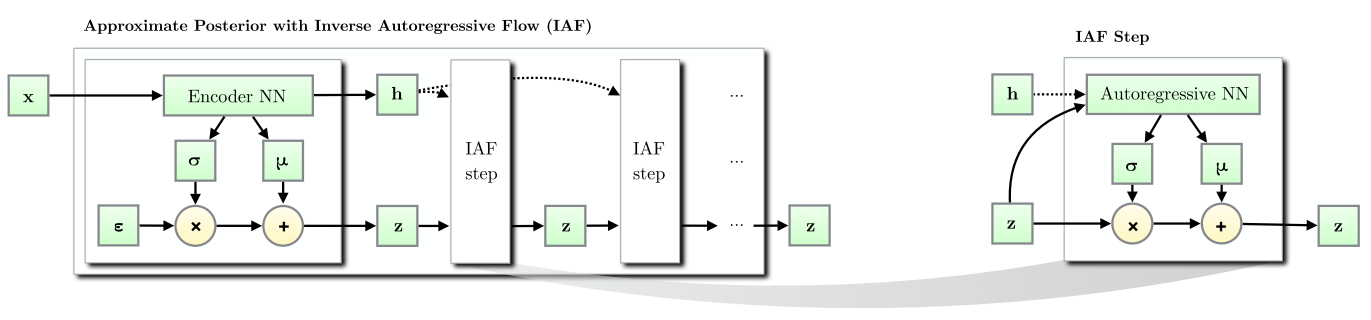
Figure 4: (Left) An Inverse Autoregressive Flow (IAF) transforming the basic posterior of an variational encoder to a more complex posterior through multiple IAF transforms. (Right) A single IAF transform. (Source: [3])
To start off, we generate our basic latent variables as we would in an vanilla VAE starting from a standard diagonal Gaussian \({\bf \epsilon} \sim \mathcal{N}(0, I)\):
where \({\bf \mu}_0, {\bf \sigma}_0\) are generated by our encoder network. So far nothing too exciting.
Now here's the interesting part, we want to apply Equation 8 as an IAF transform to go from \({\bf z}_t\) to \({\bf z}_{t+1}\) (indices refer to the number of transforms applied on the vector \(\bf z\), not the index into \(\bf z\)) but there are a few issues we need to resolve first. Let's start with reinterpreting Equation 8, rewriting it in terms of \({\bf z}_t\) and \({\bf z}_{t+1}\) (we'll omit the indices into the vector with the understanding that \(\mu\) and \(\sigma\) are autoregressive):
where \({\bf s}_t = \frac{1}{{\bf \sigma}_t}\) and \({\bf m}_t = -\frac{{\bf \mu}_t}{{\bf \sigma}_t}\). We can do this re-writing because remember that we are learning these functions through a neural network so it doesn't really matter if we invert or negate.
Next, let's introduce a context \(\bf h\). Recall, our posterior is \(p({\bf z}|{\bf x})\) but this is the same as just saying \(p({\bf z}|{\bf x}, f({\bf x}))\), where \(f(\cdot)\) is some deterministic function. So let's just define \({\bf h}:=f({\bf x})\) and then use it in our IAF transforms. This is not a problem because our latent variable is still only a function of \({\bf x}\):
Equation 13 now matches Figure 4 (where we've relabelled \(\mu, \sigma\) to \(m, s\) for clarity).
The last thing to note is that in the actual implementation, [3] suggests a modification to improve numerical stability while fitting. Given the outputs of the autoregressive network:
We construct \({\bf z}_t\) as:
where sigm is the sigmoid function. This is inspired by an LSTM-style updating. They also suggest to initialize the weights of \({\bf s}_t\) to saturate the sigmoid so that it's mostly just a pass-through to start. During experimentation, I saw that if I didn't use this LSTM-style trick, by the third or fourth IAF transform I started getting NaNs really quickly.
Deriving the IAF Density
Now that we have Equation 15, we can finally derive the posterior density. Even with the change of variable above, \({\bf s}, {\bf m}\) are still autoregressive so Equation 10 applies. Using this fact, starting from Equation 5:
where \(q({\bf z}_0|{\bf x})\) is just an isotropic Gaussian centered at \({\bf \mu}_0\) with \({\bf \sigma}_0\). Here we apply Equation 3 to transform back to an expression involving just \(\bf \epsilon\), and absorb the \({\sigma}_0\) into the summation (by changing variable to \({\bf s}\)).
Lastly, we can write our entire variational objective as:
with \(\log p({\bf z_T})\) as our standard diagonal Gaussian prior and whatever distribution you want on your output variable \(\log p({\bf x}|{\bf z}_T)\) (e.g. Bernoulli, Gaussian, etc.). With Equation 17, you can just negate it and use it as your loss function for your IAF VAE (the expectation gets estimated implicitly with the mini-batches of your stochastic gradient descent).
Experiments: IAF Implementation
I implemented a VAE with IAF on both a binarized MNIST dataset as well as CIFAR10 in a set of notebooks. My implementation uses a modification of the MADE autoencoder from [2] (see my previous post on Autoregressive Autoencoders) for the IAF layers. I only used the "basic" version of the IAF network from the paper, not the extension based on ResNet. As usual, things were pretty easy to put together using Keras because I basically took the code for a VAEs, added the code I had for a MADE, and modified the loss function as needed 2.
The network for the encoder consists of a few convolution layers, a couple of dense layers, and a symmetric structure for the decoder except with transposed convolutions. I used 32 latent dimensions for MNIST and 128 for CIFAR10 with proportional number of filters and hidden nodes for the convolutional and dense layers respectively. For the IAF portion, I used separate MADE layers (with 2 hidden layers each) for the \(\bf m\) and \(\bf s\) variables with 10x hidden nodes relative to the latent dimensions. As the paper suggested, I reversed the order of \(\bf z_t\) after each IAF transform.
Model |
Training Loss |
Validation Loss |
P(x|z) Test Loss |
|---|---|---|---|
MNIST-VAE |
70.92 |
72.33 |
40.19 |
MNIST-VAE+IAF |
66.44 |
70.89 |
39.99 |
CIFAR10-VAE |
1815.29 |
1820.17 |
1781.58 |
CIFAR10-VAE+IAF |
1815.07 |
1823.05 |
1786.24 |
Table 1 shows the results of the experiments on both datasets. As you can see the IAF layers seems to do a bit of improvement on MNIST taking the validation loss down from \(72.3\) to \(70.9\), while there's barely an improvement on the test output loss. This didn't really have any affect on the generated images, which qualitatively showed no difference. The IAF layers seemed improve the MNIST numbers a bit but only marginally.
The CIFAR10 results seemed to get worse on validation/test sets. One thing that I did notice is that adding more IAF layers requires more training (there are many more parameters) and also you need some "tricks" in order to properly train it. This is likely due to the long chain of dense layers that make up the IAF transforms, similar to troubles you might have in an LSTM. So it's quite possible that the IAF layers could be slightly beneficial but I just didn't train it quite right.
My overall conclusion is that IAF didn't seem to have a huge affect on the resulting output (at least on its own). I was hoping that it would help VAEs achieve GAN-like results but alas, it's not quite there. I will note that [3] actually had a novel architecture using IAF transforms with a ResNet like structure. This is where they achieved near state-of-the-art results on CIFAR10. Probably this structure is much easier to train (like ResNet) and really allows you to take advantage of the IAF layers.
Implementation Notes
The "context" vector is connected to the input of the MADE with an additional dense layer (see implementation).
The trick from Equation 15 was needed. Even at 4 IAF layers I started getting NaNs pretty quickly.
-
Even beyond Equation 15, I had a lot of trouble with getting things to be stable with the MADE computations, not sure if all of them helped:
Added regularizers on the MADE layers.
Used 'sigmoid' for activation for all MADE stuff (instead of the 'elu' activation I used for the other layers).
I disabled dropout for all layers.
I had a bunch of confusion with the \(\log q(z|x)\) computation, especially the determinant. Only after I worked through the math did I actually figure out the sign of the determinant in Equation 17. The key is really understanding the change of variables in Equation 12.
I actually spent a lot of time trying to get IAFs to work on a "toy" example using various synthetic data like mixed Gaussians or weird auto-regressive distributions. In all these cases, I had a lot of trouble showing that the IAF transforms did anything, it looks to perform pretty much on par with a vanilla VAE. My hypothesis on this is that either the distributions were too simple so the vanilla VAE works really well, or the IAF transforms don't do much. I suspect the latter is probably most of it.
Now I'm wondering if the normalizing flow transforms from [1] will do a better job but I didn't spend any time trying to implement it to see if it made a difference.
Conclusion
Well there you have, another autoencoder post! When I first read about this idea I was super excited because conceptually it's so beautiful! Using the exact same VAE that we all know and love, you can improve its performance just by transforming the posterior and removing the big perceived limitation: diagonal Gaussians. Unfortunately, normalizing flows with IAF transforms are no silver bullet and the improvements I saw were pretty small (if you know otherwise please let me know!). Despite this, I still really like the idea, at least theoretically, because I think it really shows some creativity to use the inverse of an autoregressive flow in addition to the whole concept of a normalizing flow. Who knew transforming probability distributions would be useful? Anyways, I learned lots of really interesting things working on this and you can expect more in the new year! Happy Holidays!
Further Reading
Previous posts: Variational Autoencoders, A Variational Autoencoder on the SVHN dataset, Semi-supervised Learning with Variational Autoencoders, Autoregressive Autoencoders
My implementation on Github: notebooks
[1] "Variational Inference with Normalizing Flows", Danilo Jimenez Rezende, Shakir Mohamed, ICML 2015
[2] "MADE: Masked Autoencoder for Distribution Estimation", Germain, Gregor, Murray, Larochelle, ICML 2015
[3] "Improving Variational Inference with Inverse Autoregressive Flow", Diederik P. Kingma, Tim Salimans, Rafal Jozefowicz, Xi Chen, Ilya Sutskever, Max Welling, NIPS 2016
[4] "Tutorial on Variational Autoencoders", Carl Doersch, http://arxiv.org/abs/1606.05908
Wikipedia: Probability Density Function: Dependent variables and change of variables
Github code for "Improving Variational Inference with Inverse Autoregressive Flow": https://github.com/openai/iaf/
- 1
-
At least by my estimate the results are kind of marginal. Improving the posterior on its own doesn't seem to have a significant boost in the ELBO or the output variable likelihood. The IAF paper [3] actually does have really good results on CIFAR10 but uses a novel architecture combined with IAF transforms. But by itself, the IAF doesn't seem to do that much.
- 2
-
Actually, it was a bit harder than that because I had to work through a bunch of bugs and misinterpretations of the math, but the number of lines added was quite small.