Autoregressive Autoencoders
You might think that I'd be bored with autoencoders by now but I still find them extremely interesting! In this post, I'm going to be explaining a cute little idea that I came across in the paper MADE: Masked Autoencoder for Distribution Estimation. Traditional autoencoders are great because they can perform unsupervised learning by mapping an input to a latent representation. However, one drawback is that they don't have a solid probabilistic basis (of course there are other variants of autoencoders that do, see previous posts here, here, and here). By using what the authors define as the autoregressive property, we can transform the traditional autoencoder approach into a fully probabilistic model with very little modification! As usual, I'll provide some intuition, math and an implementation.
Vanilla Autoencoders
The basic autoencoder is a pretty simple idea. Our primary goal is take an input sample \(x\) and transform it to some latent dimension \(z\) (encoder), which hopefully is a good representation of the original data. As usual, we need to ask ourselves: what makes a good representation? An autoencoder's answer: "A good representation is one where you can reconstruct the original input!". The process of transforming the latent dimension \(z\) back to a reconstructed version of the input \(\hat{x}\) is called the decoder. It's an "autoencoder" because it's using the same value \(x\) value on the input and output. Figure 1 shows a picture of what this looks like.
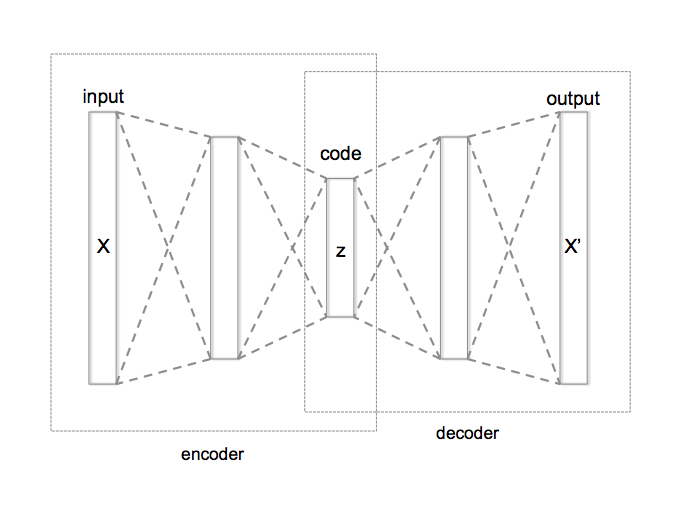
Figure 1: Vanilla Autoencoder (source: Wikipedia)
From Figure 1, we typically will use a neural network as the encoder and a different (usually similar) neural network as the decoder. Additionally, we'll typically put a sensible loss function on the output to ensure \(x\) and \(\hat{x}\) are as close as possible:
Here we assume that our data point \({\bf x}\) has \(D\) dimensions. The loss function we use will depend on the form of the data. For binary data, we'll use cross entropy and for real-valued data we'll use the mean squared error. These correspond to modelling \(x\) as a Bernoulli and Gaussian respectively (see the box).
Negative Log-Likelihoods (NLL) and Loss Functions
The loss functions we typically use in training machine learning models are usually derived by an assumption on the probability distribution of each data point (typically assuming identically, independently distributed (IID) data). It just doesn't look that way because we typically use the negative log-likelihood as the loss function. We can do this because we're usually just looking for a point estimate (i.e. optimizing) so we don't need to worry about the entire distribution, just a single point that gives us the highest probability.
For example, if our data is binary, then we can model it as a Bernoulli with parameter \(p\) on the interval \((0,1)\). The probability of seeing a given 0/1 \(x\) value is then:
If we take the logarithm and negate it, we get the binary cross entropy loss function:
This is precisely the expression from Equation 1, except we replace \(x=x_i\) and \(p=\hat{x_i}\), where the former is the observed data and latter is the estimate of the parameters that our model gives.
Similarly, we can do the same trick with a normal distribution. Given an observed real-valued data point \(x\), the probability density for parameters \(\mu, \sigma^2\) is given by:
Taking the negative logarithm of this function, we get:
Now if we assume that the variance is the same fixed value for all our data points, then the only parameter we're optimizing for is \(\mu\). So adding and multiplying a bunch of constants to our main expression doesn't change the optimal (highest probability) point so we can just simplify it (when optimizing) and still get the same point solution:
Here our observation is \(x\) and our model would produce an estimate of the parameter \(\mu\) i.e. \(\hat{x}\) in this case. I have some more details on this in one of my previous posts on regularization.
Losing Your Identity
Now this is all well and good but an astute observer will notice that unless we put some additional constraints, our autoencoder can just set \(z=x\) (i.e. the identity function) and generate a perfect reconstruction. What better representation for a reconstruction than exactly the original data? This is not desirable because we originally wanted to find a good latent representation for \(z\), not just regurgitate \(x\)! We can easily solve this though by making it difficult to learn just the identity function.
The easiest method is to just make the dimensions of \(z\) smaller than \(x\). For example, if your image has 900 pixels (30 x 30) then make the dimensions of \(z\), say 100. In this way, you're "forcing" the autoencoder to learn a more compact representation.
Another method used in denoising autoencoders is to artificially introduce noise on the input \(x' = \text{noise}(x)\) (e.g. Gaussian noise) but still compare the output of the decoder with the clean value of \(x\). The intuition here is that a good representation is robust to any noise that you might give it. Again, this prevents the autoencoder from just learning the identify mapping (because your input is not the same as your output anymore).
In both cases, you will eventually end up with a pretty good latent representation of \(x\) that can be used in all sorts of applications such as semi-supervised learning.
A Not-So-Helpful Probabilistic Interpretation
Although vanilla autoencoders can do pretty well in learning a latent representation of the data in an unsupervised manner, they don't have a useful probabilistic interpretation. We put a loss function on the outputs of the autoencoder in Equation 1 and 2 but that only leads to a trivial probabilistic distribution! Let me explain.
Ideally, we would like the unsupervised autoencoder to learn the distribution of the data. That is, we would like to be able to approximate the marginal probability distribution \(P({\bf x})\), which let's us do a whole bunch of useful and interesting things (e.g. sampling). Our autoencoder, however, does not model the marginal distribution, it models the conditional distribution given inputs \(\bf x_i\) (subscript denoting data point \(i\)). Thus, our network is actually modelling \(P({\bf x} | {\bf x_i})\) -- a conditional probability distribution that is approximately centred on \(x_i\), given that same data point as input.
This is weird in two ways. First, this conditional distribution is kind of fictional -- \(x_i\) is a single data point, so it doesn't really make sense to talk about a distribution centred on it. While you could argue it might have some relation to the other data points, the chances that the Bernoulli or Gaussian in Equation 1 and 2 model that correctly are pretty slim. Second, the bigger problem is that you are giving \(x_i\) as input to try to generate a distribution centred on \(x_i\)! You don't need a neural network to do that! You can just pick a variance and slap an independent normal distribution on each output (for the continuous case). As we can see, trying to interpret this vanilla autoencoder network using the lens of probability is not very useful.
The more typical way you might want to actually use an autoencoder network is by just using the decoder network. In this setting, you have a distribution conditional on the latent variables \(P({\bf x}|{\bf z})\). This is pretty much the setup we have in variational autoencoders (with some extra details outlined in the linked post). However, with vanilla autoencoders we have no probabilistic interpretation of the latent variable \(z\), thus still do not have a useful probabilistic interpretation.
For vanilla autoencoders, we started with some neural network and then tried to apply some sort of probabilistic interpretation that didn't quite work out. Why not do it the other way around: start with a probabilistic model and then figure out how to use neural networks to help you add more capacity and scale it?
Autoregressive Autoencoders
So vanilla autoencoders don't quite get us to a proper probability distribution but is there a way to modify them to get us there? Let's review the product rule:
where \({\bf x}_{<i} = [x_1, \ldots, x_{i-1}]\). Basically, component \(i\) of \({\bf x}\) only depends on the dimensions of \(j < i\).
So how does this help us? In vanilla autoencoders, each output \(\hat{x_i}\) could depend on any of the components input \(x_1,\ldots,x_n\), as we saw before, this resulted in an improper probability distribution. If we start with the product rule, which guarantees a proper distribution, we can work backwards to map the autoencoder to this model.
For example, let's consider binary data (say a binarized image). \(\hat{x_1}\) does not depend on any other components of \({\bf x}\), therefore our implementation should just need to estimate a single parameter \(p_1\) for this pixel. How about \(\hat{x_2}\) though? Now we let \(\hat{x_2}\) depend only on \(x_1\) since we have \(p(x_2|x_1)\). This dependency can be modelled using a non-linear function... say maybe a neural network? So we'll have some neural net that maps \(x_1\) to the \(\hat{x_2}\) output. Now consider the general case of \(\hat{x_j}\), we can have a neural net that maps \(\bf x_{<j}\) to the \(\hat{x_j}\) output. Lastly, there's no reason that each step needs to be a separate neural network, we can just put it all together in a single shared neural network so long as we follow a couple of rules:
Each output of the network \(\hat{x}_i\) represents the probability distribution \(p(x_i|{\bf x_{<i}})\).
Each output \(\hat{x_i}\) can only have connections (recursively) to smaller indexed inputs \(\bf x_{<i}\) and not any of the other ones.
Said another way, our neural net first learns \(p(x_1)\) (just a single parameter value in the case of binarized data), then iteratively learns the function mapping from \({\bf x_{<j}}\) to \(x_j\). In this view of the autoencoder, we are sequentially predicting (i.e. regressing) each dimension of the data using its previous values, hence this is called the autoregressive property of autoencoders.
Now that we have a fully probabilistic model that uses autoencoders, let's figure out how to implement it!
Masks and the Autoregressive Network Structure
The autoregressive autoencoder is referred to as a "Masked Autoencoder for Distribution Estimation", or MADE. "Masked" as we shall see below and "Distribution Estimation" because we now have a fully probabilistic model. ("Autoencoder" now is a bit looser because we don't really have a concept of encoder and decoder anymore, only the fact that the same data is put on the input/output.)
From the autoregressive property, all we want to do is ensure that we only have connections (recursively) from inputs \(i\) to output \(j\) where \(i < j\). One way to accomplish this is to not make the unwanted connections in the first place, but that's a bit annoying because we can't easily use our existing infrastructure for neural networks.
The main observation here is that a connection with weight zero is the same as no connection at all. So all we have to do is zero-out the weights we don't want. We can do that easily with a "mask" for each weight matrix which says which connections we want and which we don't.
This is a simple modification to our standard neural networks. Consider a one hidden layer autoencoder with input \(x\):
where:
\(\odot\) is an element wise product
\(\bf x, \hat{x}\) is our vectors of input/output respectively
\(\bf h(x)\) is the hidden layer
\(\bf g(\cdot)\) is the activation function of the hidden layer
\(\text{sigm}(\cdot)\) is the sigmoid activation function of the output layer
\(\bf b, c\) are the constant biases for the hidden/output layer respectively
\(\bf W, V\) are the weight matrices for the hidden/output layer respectively
\(\bf M^W, M^V\) are the weight mask matrices for the hidden/output layer respectively
So long as our masks are set such that the autoregressive property is satisfied, the network can produce a proper probability distribution. One subtlety here is that for each hidden unit, we need to define an index that says which inputs it can be connected to (which also determines which index/output in the next layer it can be connected to). We'll use the notation in the paper of \(m^l(k)\) to denote the index assigned to hidden node \(k\) in layer \(l\). Our general rule for our masks is then:
Basically, for a given node, only connect it to nodes in the previous layer that have an index less than or equal to its index. This will guarantee that a given index will recursively obey our auto-regressive property.
The output mask has a slightly different rule:
which replaces the less than equal with just an equal. This is important because the first node should not depend on any other ones so it should not have any connections (will only have the bias connection), and the last node can have connections (recursively) to every other node except its respective input.
Finally, one last topic to discuss is how to assign \(m^l(k)\). It doesn't really matter too much as long as you have enough connections for each index. The paper did a natural thing and just sampled from a uniform distribution with range \([1, D-1]\). Why only up to \(D-1\)? Recall, we should never assign index \(D\) because it will never be used so there's no use in connecting anything to \(D\) (nothing can ever depend on the \(D^{\text{th}}\) input). Figure 2 (from the original paper) shows this whole process pictorially.
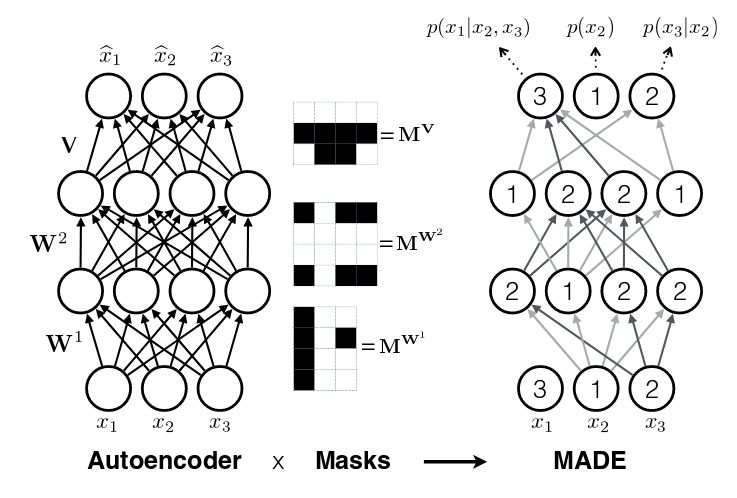
Figure 2: MADE Masks (Source: [1])
A few things to notice:
Output 1 is not connected to anything. It will just be estimated with a single constant parameter derived from the bias node.
Input 3 is not connected to anything because no node should depend on it (autoregressive property).
\(m^l(k)\) are more or less assigned randomly.
If you trace back from output to input, you will see that the autoregressive property is maintained.
So then implementing MADE is as simple as providing a weight mask and doing an extra element-wise product. Pretty simple, right?
Ordering Inputs, Masks, and Direct Connections
A few other minor topics that can improve the performance of the MADE. The first is the ordering of the inputs. We've been taking about "Input 1, 2, 3, ..." but usually there is no natural ordering of the inputs. We can arbitrarily pick any ordering that we want just by shuffling \({\bf m^0}\), the selection layer for the input. This can even be performed at each mini-batch to get an "average" over many different models.
The next idea is also very similar, instead of just resampling the input selection, resample all \({\bf m^L}\) selections. In the paper, they mention the best results are having a fixed number of configurations for these selections (and their corresponding masks) and rotating through them in the mini-batch training.
The last idea is just to add a direct connection path from input to output like so:
where \({\bf A}\) is the weight matrix that directly connects inputs to outputs, and \({\bf M^A}\) is the corresponding mask matrix that follows the autoregressive property.
Generating New Samples
One final idea that isn't explicitly mentioned in the paper is how to generate new samples. Remember, we now have a fully generative probabilistic model for our autoencoder. It turns out it's quite easy but a bit slow. The main idea (for binary data):
Randomly generate vector \({\bf x}\), set \(i=1\).
Feed \({\bf x}\) into autoencoder and generate outputs \(\hat{\bf x}\) for the network, set \(p=\hat{x_i}\).
Sample from a Bernoulli distribution with parameter \(p\), set input \(x_{i}=\text{Bernoulli}(p)\).
Increment \(i\) and repeat steps 2-4 until i > D.
Basically, we're iteratively calculating \(p(x_i|{\bf x_{<i}})\) by doing a forward pass on the autoencoder each time. Along the way, we sample from the Bernoulli distribution and feed the sampled value back into the autoencoder to compute the next parameter for the next bit. It's a bit inefficient but MADE is also a relatively small modification to the vanilla autoencoder so you can't ask for too much.
MADE Implementation
I implemented a MADE layer and built a network using a binarized MNIST dataset similar to what they used in the original paper (notebook).
My implementation is a lot simpler than the one used in the paper. I used Keras and created a custom "MADE" layer that took as input the number of layers, number of hidden units per layer, whether or not to randomize the input selection, as well as standard stuff like dropout and activation function. I didn't implement any of the randomized masks for minibatchs because it was a bit of a pain. I did implement the direct connection though.
(As an aside: I'm really a big fan of higher-level frameworks like Keras, it's quite wonderful. The main reason is that for most things I have the nice Keras frontend, and then occasionally I can dip down into the underlying primitives when needed via the Keras "backend". I suspect when I eventually get around to playing with RNNs it's not going to be as wonderful but for now I quite like it.)
I was able to generate some new digits that are not very pretty, shown in Figure 3.

Figure 3: Generated MNIST images using Autoregressive Autoencoder
It's a bit hard to make out any numbers here. If you squint hard enough, you can make out some "4"s, "3"s, "6"s, maybe some "9"s? The ones in the paper look a lot better (although still not perfect, there were definitely some that were hard to make out).
The other thing is that I didn't use their exact version of binarized MNIST, I just took the one from Keras and did a round() on each pixel. This might also explain why I was unable to get as good of a negative log-likelihood as them. In the paper they report values \(< 90\) (even with a single mask) but the lowest I was able to get on my test set was around \(99\), and that was after a bunch of tries tweaking the batch and learning rate (more typical was around \(120\)). It could be that their test set was easier, or the fact that they did some hyper-parameter tuning for each experiment, whereas I just did some trial and error tuning.
Implementation Notes
Here are some random notes that I came across when building this MADE:
Adding a direct (auto-regressive) connection between inputs and outputs seemed to make a huge difference (150 vs. < 100 loss). For me, this basically was the make-or-break piece for implementing a MADE. It's funny that it's just a throw-away paragraph in the actual paper. Probably because the idea was from an earlier paper in 2000 and not the main contribution of the paper. For some things, you really have to implement it to understand the important parts, papers don't tell the whole story!
I had to be quite careful when coding up layers since getting the indexes for selection exactly right is important. I had a few false starts because I mixed up the indexes. When using the high-level Keras API, there's not much of this detailed work, but when implementing your own layers it's important!
I tried a random ordering (just a single one for the entire training, not one per batch) and it didn't really seem to do much.
In their actual implementation, they also add dropout to all their layers. I added it too but didn't play around with it much except to try to tune it to get a lower NLL. One curious thing I found out was about using the set_learning_phase() API. When implementing dropout, I basically just took the code from the dropout layer and inserted into my custom layer. However, I kept getting an error, it turns out that I had to use set_learning_phase(1) during training, and set_learning_phase(0) during prediction because the Keras dropout implementation uses in_train_phase(<train_input>, <test_input>), which switches between two behaviours for training/testing based on the status of this bit. For some reason when using the regular dropout layer you don't have to do this but when doing it in a custom layer you do? I suspect I missed something in my custom layer that happens in the dropout layer.
Conclusion
So yet another post on autoencoders, I can't seem to get enough of them! Actually I still find them quite fascinating, which is why I'm following this line of research about fully probabilistic generative models. There's still at least one or two more papers in this area that I'm really excited to dig into (at which point I'll have approached the latest published work), so expect more to come!
Further Reading
Previous posts: Variational Autoencoders, A Variational Autoencoder on the SVHN dataset, Semi-supervised Learning with Variational Autoencoders
My implementation on Github: notebook
[1] "MADE: Masked Autoencoder for Distribution Estimation", Germain, Gregor, Murray, Larochelle, ICML 2015
Wikipedia: Autoencoder
Github code for "MADE: Masked Autoencoder for Distribution Estimation", https://github.com/mgermain/MADE