Tensors, Tensors, Tensors
This post is going to take a step back from some of the machine learning topics that I've been writing about recently and go back to some basics: math! In particular, tensors. This is a topic that is casually mentioned in machine learning papers but for those of us who weren't physics or math majors (*cough* computer engineers), it's a bit murky trying to understand what's going on. So on my most recent vacation, I started reading a variety of sources on the interweb trying to piece together a picture of what tensors were all about. As usual, I'll skip the heavy formalities (partly because I probably couldn't do them justice) and instead try to explain the intuition using my usual approach of examples and more basic maths. I'll sprinkle in a bunch of examples and also try to relate it back to ML where possible. Hope you like it!
A Tensor by Any Other Name
For newcomers to ML, the term "tensor" has to be one of the top ten confusing terms. Not only because the term is new, but also because it's used ambiguously with other branches of mathematics and physics! In ML, it's colloquially used interchangeably with a multidimensional array. That's what people usually mean when they talk about "tensors" in the context of things like TensorFlow. However, tensors as multidimensional arrays is just one very narrow "view" of a tensor, tensors (mathematically speaking) are much more than that! Let's start at the beginning.
(By the way, you should checkout [1], which is a great series of videos explaining tensors from the beginning. It definitely helped clarify a lot of ideas for me and a lot of this post is based on his presentation.)
Geometric Vectors as Tensors
We'll start with a concept we're all familiar with: geometric vectors (also called Euclidean vectors). Now there are many different variants of "vectors" but we want to talk specifically about the geometric vectors that have a magnitude and direction. In particular, we're not talking about just an ordered pair of numbers (e.g. \([1, 2]\) in 2 dimensions).
Of course, we're all familiar with representing geometric vectors as ordered pairs but that's probably because we're just assuming that we're working in Euclidean space where each of the indices represent the component of the basis vectors (e.g. \([1, 0]\) and \([0, 1]\) in 2 dimensions). If we change basis to some other linearly independent basis, the components will change, but will the magnitude and direction change? No! It's still the same old vector with the same magnitude and direction. When changing basis, we're just describing or "viewing" the vector in a different way but fundamentally it's still the same old vector. Figure 1 shows a visualization.
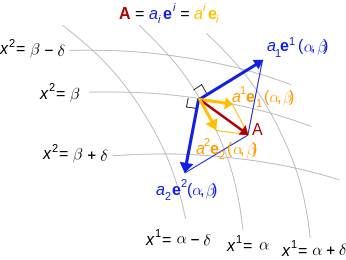
Figure 1: The geometric vector A (in red) is the same regardless of what basis you use (source: Wikipedia).
You can see in Figure 1 that we have a vector \(A\) (in red) that can be represented in two different bases: \(e^1, e^2\) (blue) and \(e_1, e_2\) (yellow) 1. You can see it's the same old vector, it's just that the way we're describing it has changed. In the former case, we can describe it as a coordinate vector by \([a_1, a_2]\), while in the latter by the coordinate vector \([a^1, a^2]\) (note: the super/subscripts represent different values, not exponents, which we'll get to later, and you can ignore all the other stuff in the diagram).
So then a geometric vector is the geometric object, not specifically its representation in a particular basis.
Example 1: A geometric vector in a different basis.
Let's take the vector \(v\) as \([a, b]\) in the standard Euclidean basis: \([1, 0]\) and \([0, 1]\). Another way to write this is as:
Now what happens if we scale our basis by \(2\)? This can be represented by multiplying our basis matrix (where each column is one of our basis vectors) by a transformation matrix:
So our new basis is \([2, 0]\) and \([0, 2]\). But how does our original vector \(v\) get transformed? We actually have to multiply by the inverse scaling matrix:
So our vector is represented as \([\frac{a}{2}, \frac{b}{2}]\) in our new basis. We can see that this results in the exact same vector regardless of what basis we're talking about:
Now let's do a more complicated transform on our Euclidean basis. Let's rotate the axis by 45 degrees, the transformation matrix is this:
The inverse of our rotation matrix is:
Therefore our vector \(v\) can be represented in this basis (\([\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}], [-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]\)) as:
Which we can see is exactly the same vector as before:
So Example 1 shows us how a vector represents the same thing regardless of what basis you happen to be working in. As you might have guessed, these geometric vectors are tensors! Since it has one physical axis, it is said to be a rank=1 tensor. A scalar is said to be a rank=0 tensor, which is pretty much just a degenerate case. Note: rank is different than dimension.
In physics and other domains, you may want to work in a non-standard Euclidean basis because it's more convenient, but still want to talk about the same objects regardless if we're in a standard basis or not.
So geometric vectors are our first step in understanding tensors. To summarize some of the main points:
Tensors can be viewed as an ordered list of numbers with respect to a basis but that isn't the tensor itself.
They are independent of a change in basis (i.e. their representation changes but what they represent does not).
The rank (or degree or order) of a tensor specifies how many axes you need to specify it (careful this is different than the dimensional space we're working in).
Just to drive the first point home, Example 2 shows an example of a tuple that might look like it represents a tensor but does not.
Example 2: Non-Tensors
We can represent the height, width and length of a box as an ordered list of numbers: \([10, 20, 15]\). However, this is not a tensor because if we change our basis, the height, width and length of the box don't change, they stay the same. Tensors, however, have specific rules of how to change their representation when the basis changes. Therefore, this tuple is not a tensor.
Covariant vs. Contravariant Tensors
In the last section, we saw how geometric vectors as tensors are invariant to basis transformations and how you have to multiply the inverse of the basis transformation matrix with the coordinates in order to maintain that invariance (Example 1). Well it turns out depending on the type of tensor, how you "maintain" the invariance can mean different things.
A geometric vector is an example of a contravariant vector because when changing basis, the components of the vector transform with the inverse of the basis transformation matrix (Example 1). It's easy to remember it as "contrary" to the basis matrix. As convention, we will usually label contravariant vectors with a superscript and write them as column vectors:
In Equation 9, \(\alpha\) is not an exponent, instead we should think of it as a "loop counter", e.g. \(\text{for } \alpha \text{ in } 0 .. 2\). Similarly, the superscripts inside the vector correspond to each of the components in a particular basis, indexing the particular component. We'll see a bit later why this notation is convenient.
As you might have guessed, the other type of vector is a covariant vector (or covector for short) because when changing basis, the components of the vector transform with the same basis transformation matrix. You can remember this one because it "co-varies" with the basis transformation. As with contravariant vectors, a covector is a tensor of rank 1. As convention, we will usually label covectors with a subscript and write them as a row vectors:
Now covectors are a little bit harder to explain than contravariant vectors because the examples of them are more abstract than geometric vectors 2. First, they do not represent geometric vectors (or else they'd be contravariant). Instead, we should think of them as a linear function that takes a vector as input (in a particular basis) and maps it to a scalar, i.e.:
This is an important idea: a covariant vector is an object that has an input (vector) and produces an output (scalar), independent of the basis you are in. In contrast, a contravariant vector like a geometric vector, takes no input and produces an output, which is just itself (the geometric vector). This is a common theme we'll see in tensors: input, output, and independent of basis. Let's take a look at an example of how covectors arise.
Example 3: A differential as a Covariant Vector
Let's define a function and its differential in \(\mathbb{R}^2\) in the standard Euclidean basis:
If we are given a fixed point \((x_0,y_0) = (1,2)\), then the differential evaluated at this point is:
where in the last equation, I just relabelled things in terms of \(g, x, \text{ and } y\) respectively, which makes it look exactly like a linear functional!
As we would expect with a tensor, the "behaviour" of this covector shouldn't really change even if we change basis. If we evaluate this functional at a geometric vector \(v=(a, b)\) in the standard Euclidean basis, then of course we get \(g(a,b)=2a + 4b\), a scalar. If this truly is a tensor, this scalar should not change even if we change our basis.
Let's rotate the axis 45 degrees. From example 1, we know the rotation matrix and the inverse of it:
To rotate our original point \((a,b)\), we multiply the inverse matrix by the column vector as in Equation 7 to get \(v\) in our new basis, which we'll denote by \(v_{R}\):
If you believe what I said before about covectors varying with the basis change, then we should just need to multiply our covector, call it \(u = [2, 4]\) (as a row vector in the standard Euclidean basis) by our transformation matrix:
Evaluating \(v_R\) at \(u_R\):
which is precisely the scalar that we got in the Euclidean basis.
Before we move on, I want to introduce some more notation to simply our lives. From Equation 11, using some new notation, we can re-write covector \(u_\alpha\) with input geometric vector \(v^\alpha\) (specified by their coordinates in the same basis) as:
Note as before the superscripts are not exponentials but rather denote an index. The last expression uses the Einstein summation convention: if the same "loop variable" appears once in both a lower and upper index, it means to implicitly sum over that variable. This is standard notation in physics textbooks and makes the tedious step of writing out summations much easier. Also note that covectors have a subscript and contravariant vectors have a superscript, which allows them to "cancel out" via summation. This becomes more important as we deal with higher order tensors.
One last notational point is that we now know of two types of rank 1 tensors: contravariant vectors (e.g. geometric vectors) and covectors (or linear functionals). Since they're both rank 1, we need to be a bit more precise. We'll usually write of a \((n, m)\)-tensor where \(n\) is the number of contravariant components and \(m\) is the number of covariant components. The rank is then the sum of \(m+n\). Therefore a contravariant vector is a \((1, 0)\)-tensor and a covector is a \((0, 1)\)-tensor.
Linear Transformations as Tensors
Another familiar transformation that we see is a linear transformation (also called a linear map). Linear transformations are just like we remember from linear algebra, basically matrices. But a linear transformation is still the same linear transformation when we change basis so it is also a tensor (with a matrix view being one view).
Let's review a linear transformation:
A function \(L:{\bf u} \rightarrow {\bf v}\) is a linear map if for any two vectors \(\bf u, v\) and any scalar c, the following two conditions are satisfied (linearity):
\begin{align*} L({\bf u} + {\bf v}) &= L({\bf u}) + L({\bf v}) \\ L(c{\bf u}) &= cL({\bf u}) \tag{19} \end{align*}
One key idea here is that a linear transformation takes a vector \(\bf v\) to another vector \(L(\bf v)\) in the same basis. The linear transformation itself has nothing to do with the basis (we of course can apply it to a basis too). Even though the "output" is a vector, it's analogous to the tensors we saw above: an object that acts on a vector and returns something, independent of the basis.
Okay, so what kind of tensor is this? Let's try to derive it! Let's suppose we have a geometric vector \(\bf v\) and its transformed output \({\bf w} = L{\bf v}\) in an original basis, where \(L\) is our linear transformation (we'll use matrix notation here). After some change in basis via a transform \(T\), we'll end up with the same vector in the new basis \(\bf \tilde{v}\) and the corresponding transformed version \(\tilde{\bf w} = \tilde{L}{\bf \tilde{v}}\). Note that since we're in a new basis, we have to use a new view of \(L\), which we label as \(\tilde{L}\).
The second last line comes from the fact that we're going from the new basis to the old basis so we use the inverse of the inverse -- the original basis transform.
Equation 20 tells us something interesting, we're not just multiplying by the inverse transform (contravariant), nor just the forward transform (covariant), we're doing both, which hints that this is a (1,1)-tensor! Indeed, this is our first example of a rank 2 tensor, which usually is represented as a matrix (e.g. 2 axes).
Example 4: A Linear Transformation as a (1,1)-Tensor
Let's start with a simple linear transformation in our standard Euclidean basis:
Next, let's use the same 45 degree rotation for our basis as Example 1 and 2 (which also happens to be a linear transformation):
Suppose we're applying \(L\) to a vector \({\bf v}=(a, b)\), and then changing it into our new basis. Recall, we would first apply \(L\), then apply a contravariant (inverse matrix) transform to get to our new basis:
Equation 7 tells us what \(\tilde{\bf v} = R^{-1}{\bf v}\) is in our new basis:
Applying Equation 20 to \(L\) gives us:
Applying \(\tilde{L}\) to \(\tilde{\bf v}\):
which we can see is the same as Equation 23.
Bilinear Forms
We'll start off by introducing a not-so-familiar idea (at least by name) called the bilinear form. Let's take a look at the definition with respect to vector spaces:
A function \(B:{\bf u, v} \rightarrow \mathbb{R}\) is a bilinear form for two input vectors \(\bf u, v\), if for any other vector \(\bf w\) and scalar \(\lambda\), the following conditions are satisfied (linearity):
\begin{align*} B({\bf u} + {\bf w}, {\bf v}) &= B({\bf u}, {\bf v}) + B({\bf w}, {\bf v}) \\ B(\lambda{\bf u}, {\bf v}) &= \lambda B({\bf u}, {\bf v})\\ B({\bf u}, {\bf v} + {\bf w}) &= B({\bf u}, {\bf v}) + B({\bf u}, {\bf w}) \\ B({\bf u}, \lambda{\bf v}) &= \lambda B({\bf u}, {\bf v})\\ \tag{27} \end{align*}
All this is really saying is that we have a function that maps two geometric vectors to the real numbers, and that it's "linear" in both its inputs (separately, not at the same time) , hence the name "bilinear". So again, we see this pattern: a tensor takes some input and maps it to some output that is independent of a change in basis.
Similar to linear transformations, we can represent bilinear forms as a matrix \(A\):
where in the last expression I'm using Einstein notation to indicate that \(A\) is a rank (0, 2)-tensor, and \({\bf u, v}\) are both (1, 0)-tensors (contravariant).
So let's see how we can show that this is actually a (0, 2)-tensor (two covector components). We should expect that when changing basis we'll need to multiply by the basis transform twice ("with the basis"), along the same lines as the linear transformation in the previous section, except with two covector components now. We'll use Einstein notation here, but you can check out Appendix A for the equivalent matrix multiplication operation.
Let \(B\) be our bilinear, \(\bf u, v\) geometric vectors, \(T\) our basis transform, and \(\tilde{B}, \tilde{\bf u}, \tilde{\bf v}\) our post-transformed bilinear form and vectors, respectively. Here's how we can show that the bilinear transforms like a (0,2)-tensor:
As you can see we transform "with" the change in basis, so we get a (0, 2)-tensor. Einstein notation is also quite convenient (once you get used to it)!
The Metric Tensor
Before we finish talking about tensors, I need to introduce to you one of the most important tensors around: the Metric Tensor. In fact, it's probably one of the top reasons people start to learn about tensors (and the main motivation for this post).
The definition is a lot simpler because it's just a special kind of bilinear 3:
A metric tensor at a point \(p\) is a function \(g_p({\bf x}_p, {\bf y}_p)\) which takes a pair of (tangent) vectors \({\bf x}_p, {\bf y}_p\) at \(p\) and produces a real number such that:
\(g_p\) is bilinear (see previous definition)
\(g_p\) is symmetric: \(g_p({\bf x}_p, {\bf y}_p) = g_p({\bf y}_p, {\bf x}_p)\)
\(g_p\) is nondegenerate. For every \({\bf x_p} \neq 0\) there exists \({\bf y_p}\) such that \(g_p({\bf x_p}, {\bf y_p}) \neq 0\)
Don't worry so much about the "tangent" part, I'm glossing over parts of it which aren't directly relevant to this tensor discussion.
The metric tensor is important because it helps us (among other things) define distance and angle between two vectors in a basis independent manner. In the simplest case, it's exactly our good old dot product operation from standard Euclidean space. But of course, we want to generalize this concept a little bit so we still have the same "operation" under a change of basis i.e. the resultant scalar we produce should be the same. Let's take a look.
In Euclidean space, the dot product (whose generalization is called the inner product) for two vectors \({\bf u}, {\bf v}\) is defined as:
However, for the metric tensor \(g\) this can we re-written as:
where in the last expression I substituted the metric tensor in standard Euclidean space. That is, the metric tensor in the standard Euclidean basis is just the identity matrix:
So now that we have a dot-product-like operation, we can define our basis-independent definition of length of a vector, distance between two vectors and angle between two vectors:
The next example shows that the distance and angle are truly invariant between a change in basis if we use our new metric tensor definition.
Example 5: Computing Distance and Angle with the Metric Tensor
Let's begin by defining two vectors in our standard Euclidean basis:
Using our standard (non-metric tensor) method for computing distance and angle:
Now, let's try to change our basis. To show something a bit more interesting than rotating the axis, let's try to change to a basis of \([2, 1]\) and \([-\frac{1}{2}, \frac{1}{4}]\). To change basis (from a standard Euclidean basis), the transform we need to apply is:
As you can see, it's just concatenating the column vectors of our new basis side-by-side in this case (when transforming from a standard Euclidean space). With these vectors, we can transform our \({\bf u}, {\bf v}\) to the new basis vectors \(\tilde{\bf u}, \tilde{\bf v}\) as shown:
Before we move on, let's see if using our standard Euclidean distance function will work in this new basis:
As we can see, the Pythagorean method only works in the standard Euclidean basis (because it's orthonormal), once we change basis we have to account for the distortion of the transform.
Now back to our metric tensor, we can transform our metric tensor (\(g\)) to the new basis (\(\tilde{g}\)) using the forward "with basis" transform (switching to Einstein notation):
Calculating the angle and distance using Equation 33:
which line up with the calculations we did in our original basis.
The metric tensor comes up a lot in many different contexts (look out for future posts) because it helps define what we mean by "distance" and "angle". Again, I'd encourage you to check out the videos in [1]. He's got a dozen or so videos with some great derivations and intuition on the subject. It goes in a bit more depth than this post but still in a very clear manner.
Summary: A Tensor is a Tensor
So, let's review a bit about tensors:
A tensor is an object that takes an input tensor (or none at all in the case of geometric vectors) and produces an output tensor that is invariant under a change of basis, and whose coordinates change in a special, predictable way when changing basis.
A tensor can have contravariant and covariant components corresponding to the components of the tensor transforming against or with the change of basis.
The rank (or degree or order) of a tensor is the number of "axes" or components it has (not to be confused with the dimension of each "axis").
A \((n, m)\)-tensor has \(n\) contravariant components and \(m\) covariant components with rank \(n+m\).
We've looked at four different types of tensors:
Tensor |
Type |
Example |
|---|---|---|
Contravariant Vectors (vectors) |
(1, 0) |
Geometric (Euclidean) vectors |
Covariant Vectors |
(0, 1) |
Linear Functionals |
Linear Map |
(1, 1) |
Linear Transformations |
Bilinear Form |
(0, 2) |
Metric Tensor |
And that's all I have to say about tensors! Like most things in mathematics, the idea is actually quite intuitive but the math causes a lot of confusion, as does its ambiguous use. TensorFlow is such a cool name but doesn't exactly do tensors justice. Anyways, in the next post, I'll be continuing to diverge from the typical ML topics and write about some adjacent math-y topics that pop up in ML.
5. Further Reading
Wikipedia: Tensors, Metric Tensor, Covariance and contravariance of vectors, Vector
[1] Tensors for Beginners (YouTube playlist), eigenchris
[2] Tensors for Laypeople, Markus Hanke
[3] An Introduction for Tensors for Students of Physics and Engineering
Appendix A: Showing a Bilinear is a (0,2)-Tensor using Matrix Notation
Let \(B\) be our bilinear, \(\bf u, v\) geometric vectors, \(R\) our basis transform, and \(\tilde{B}, \tilde{\bf u}, \tilde{\bf v}\) our post-transformed bilinear and vectors, respectively. Here's how we can show that the bilinear transforms like a (0,2)-tensor using matrix notation:
Note: that we can only write out the matrix representation because we're still using rank 2 tensors. When working with higher order tensors, we can't fall back on our matrix algebra anymore.
- 1
-
This is not exactly the best example because it's showing a vector in both contravariant and tangent covector space, which is not exactly the point I'm trying to make here. But the idea is basically the same: the vector is the same object regardless of what basis you use.
- 2
-
There is a geometric interpretation of covectors are parallel surfaces and the contravariant vectors "piercing" these surfaces. I don't really like this interpretation because it's kind of artificial and doesn't have any physical analogue that I can think of.
- 3
-
Actually the metric tensor is usually defined more generally in terms of manifolds but I've simplified it here because I haven't quite got to that topic yet!